Two Arguments for Intelligent Design
06/29/15 | 41m 55s | Rating: TV-G
Elliott Sober, Professor, Department of Philosophy, UW-Madison, discusses the relationship between science and religion focusing on the “organismic design argument” and the “fine-tuning argument” which state that life could not have happened by a mindless process. Sober presents these theories in Bassam Shakhashiri’s Chemistry and Society class.
Copy and Paste the Following Code to Embed this Video:
Two Arguments for Intelligent Design
Tonight, we're going to be having a conversation with a very distinguished professor from UW Madison. Professor Elliot Sober, about one area that deals with the respectful dialogue that must take place between people who are caring enough to engage in conversations about the connection between science and religion. And I am very, very pleased that Professor Sober is here, and I would like to invite him now to come and begin his presentation. This is Professor Sober's title, and also the position that he holds here. So, Elliott? (applause) I'll get your slides up. Okay. Thank you, Bassam. It's nice to be here. Happy to have you. So when we think about the question of how science and religion are related to each other, is a huge question. It has many dimensions. I'm going to be talking about one aspect of one dimension. Now, many of you are familiar with the idea that science and religion are always and everywhere in conflict with each other. That science is all about evidence and rationality, whereas religion is about faith and the embracing of ideas when there is no evidence, really. That's an important idea about the relationship between science and religion, but historically, it's not the only one. There's a long tradition for thinking that ideas about religion, for example, the existence of God, can be defended in the same way that you would go about defending a scientific theory. And so today I'm going to talk about two of those arguments. They're both parts of this, this very old idea called the design argument, and one of them goes back hundreds of years, called the, which I call the organismic design argument. It's the idea that we observe organisms to have complicated adaptations, features that allow them to survive and reproduce in their environment, and the thought behind the organismic design argument is that these features could not have arisen by a mindless process. Rather, there had to be an intelligent designer who made organisms to be as we observe them. Long history for this one. There's a more recent argument, which has nothing to do with organisms, it has to do with large-scale features of the entire physical world. It's called the fine-tuning argument. It's an idea that was really only developed in the 20th century. But here again, the claim is that there are features of nature, the fact that the physical constants have a very special set of properties, namely, if they were even slightly different in value, no life could exist in the universe. And the argument, the version of the design argument called the fine-tuning argument, takes that fact about the physical constants to be evidence that the physical constants had to be set by an intelligent designer. So these are both design arguments. They're both arguments that begin with some observations we make of nature. They begin with some evidence, and they draw the conclusion that what we observe cannot be due to a mindless natural process. It has to be due to intelligent design. And of course, the intelligent designer that defenders of this argument have in mind, is God. So you see just from the outset, what I just said a minute ago, that this is the attempt to establish the existence of God not by saying it's a matter of faith, not reason, but rather, the opposite is going on here. The idea is to use scientific standards of reasoning and evidence to reach a conclusion, not about the existence of genes or electrons, but about the existence of God. It's in that style that we now call scientific. So, one of these is, I'm sure, very familiar to you, the ongoing controversy between intelligent design theory, creationism, and evolutionary theory, is an episode, a recent episode of this long-standing issue about the design argument for the existence of God. And in the case of the physical constants, the fine-tuning arguments, we're gonna be looking at how you go about explaining the fact that the physical constants have the values they have. It's kind of striking that several of them have those values, and furthermore, that if the values were even slightly different, life couldn't exist in the universe. So why is it that they have those values? And this part, this kind of design argument draws the conclusion that God wanted there to be life in the universe, and that's why he, or she, or it, set the constants with the values they have. So let's take them in, in order. The design argument, the organismic argument did not begin with Paley, but Paley is extremely famous as a defender of this argument that goes centuries and centuries earlier. He wrote a book called Natural Theology. What that means is theology done in the style of the natural sciences. The idea is that you establish propositions in theology not by saying it's a matter of faith, not by appealing to what's written in a sacred book, but rather by producing evidence and making a rational argument. Paley begins the book by talking about two things you might notice as you walk across a field, a heath, in England. You, you find that your foot hits a rock, and if you wonder why it's there, why the rock exists, it wouldn't occur to you to think, "Oh, an intelligent designer must have designed the rock "and put it there." You'd just say, "Well, whatever." You know, "The weather, the elements in the ground "somehow or other mindlessly interacted and bang," (claps hands) "there was this rock." No temptation to attribute its existence to an intelligent designer. But then Paley says, "Suppose you found a watch, "and you open the watch up and you notice "that the watch has many parts. "It's very accurate as a device for keeping time, "and you notice, furthermore, "that if the parts were even slightly different "in their arrangement from the way they are, "it wouldn't keep time." So the watch that you, the two properties that Paley took to distinguish the watch from the rock are the watch has a function. It's function is to keep time, and it's delicate. If the parts were even slightly different, it wouldn't be able to perform its function. And Paley says that difference between the watch and the rock make all the difference in the world. In the case of the rock, you'd never think, "Oh, it must have been put there by an intelligent designer." But when you see the watch, it's just irresistible to conclude that the watch is the result of an intelligent watch maker. So far, so good. Then Paley says, "Consider an organism. "An organism is a machine that has many more parts "than a watch has, "and those parts work together for a function. "They keep the organism alive, "they allow the organism to reproduce, "and if those parts were even slightly different "from the way they are, the organism would die." (claps hands) And just as you think it's obvious that the watch is the product of intelligent design, so too, you oughta conclude that organisms, especially the complex adaptations that organisms have, that too, must be due to intelligent design. So it's an argument for the existence of God based on an observation. The observation that organisms have complex adaptations. You notice the date here, it's 1802. Darwin publishes The Origin of Species in 1859. So Paley did not know about Darwin's theory. In 1996, Michael Behe, a defender of what he and his colleagues call intelligent design theory, which is a kind of successor idea to creationism, made the same argument about not the vertebrate eye, that's the examp, one of the famous examples that Paley talks about, but by very complicated and only relatively recently discovered features of biochemistry. So when you cut yourself, and you bleed, and then the blood coagulates and you stop bleeding, this is a very complicated biochemical reaction, and Behe says about blood coagulation what Paley said about the watch and the eye. Namely, it's a complicated adaptation. It wouldn't function properly if it were even slightly different in the arrangement of its parts. So, Michael Behe, more than a century after Darwin, is saying, "This is the correct explanation "of complex adaptations. "Darwin was wrong." Darwinian theory, the theory of evolution by natural selection, says Behe, cannot explain complex adaptations. So Paley didn't know about Darwin. Behe did, and his colleagues did, and so Paley couldn't criticize Darwinian theory. It didn't exist then, but Behe and his colleagues are trying to show that Darwinian theory cannot explain something that's fundamental to biology, namely, complex adaptations. Only an intelligent designer could have produced blood coagulation, the vertebrate eye, and so on. So they agree, Behe after Darwin, Paley before Darwin, agree on the kind of argument. The examples are different. Paley doesn't talk about blood coagulation. The chemistry wasn't known back then in 1802. But the kind of argument, the design of the argument, is the same in both cases. Now, what, why would Behe and other people think that Darwinian theory has a problem with explaining complex adaptations? Well, part of, one of the central ideas in Darwin's theory is called gradualism. It's the idea that evolution changes a population of organisms by inducing very, very small changes to accumulate. It doesn't happen all at once that organisms have no eye, and then (claps hands) bang, they start having the complex structure that we all have, the vertebrate eye. No, it has to be the result of the accumulation of very small, slight modifications, each of them beneficial to the individual that has it. If they're not beneficial, natural selection won't cause that characteristic to become more frequent in the population. So, Darwin's picture, which is still largely the picture in evolutionary biology now, is that complicated adaptations don't evolve, bang, (claps hands) in one fell swoop. Rather, they evolve by the gradual accumulation of small modifications, each favorable to the organism. That's what the, he thinks, is the problem for Darwinism. If that's how natural selection works, it's never gonna be able to prove, to cause the evolution of complex adaptations like the eye, like blood coagulation. And why is that? Here's the picture that Paley had before Darwin and Behe has now. It's a picture that I want to offer you to illustrate what the, what they have in mind, by a delicate adaptation. Delicate is my word. Behe uses the word "irreducible complexity" for this idea. So take a structure like the vertebrate eye that has a number of parts, and suppose they have the following feature. That if you just had one of those parts present, it wouldn't do you any good. If you had two of them, it wouldn't do you any good. You gotta get all of (snaps fingers) them there, and (claps hands) bang, then you can see. So the picture, this is the picture of the idea of irreducible complexity that Behe and Paley are working with. Add the parts, and it doesn't help the structure to function better until you get 'em all there. But if that's right, notice how this seems to be a problem for gradualism in the Darwinian mode. What's the advantage of having one part rather than zero? Nothing. What's the advantage of having two parts rather than one? Nothing. Only when you got all of them do you have the advantage. Well, if that's the way the eye, blood coagulation, and other adaptations are, then there's a problem for getting them to evolve by the Darwinian process of gradual natural selection. That's the idea. And you see this idea expressed in Dar, by Darwin himself. "If it could be demonstrated that any complex "organ existed, which could not possibly have been formed "by numerous, successive, slight modifications," I add, parenthetically, "each beneficial to the individual "that has them, my theory would be absolute, "would absolutely break down." But then he says, "I don't think there are cases like this "in nature." Well, let's think about that. Are there car, are there cases like this in nature where, as you add structures, nothing happens that's any good to the organism until you get to the end and you get all the parts present? Well here's an example, it's not about biology, it's about building an arch. So here's an arch that's made of blocks. There's no mortar gluing these blocks together. They can slide against each other. And I hope, and you see at the top, there's the keystone. And I hope it's kind of plausible to think there's no way you could build this arch one block at a time. You put the first one down here and put the next one on top of it, luilgh. Slides off, crashes to the ground. You see the problem. So it looks like this is a simple example of the idea of delicacy that Behe and Paley both had in mind. There's no gradual step-by-step process that allows you, by adding one block after another, to come up with that. So it looks like arches have to be built by an intelligent designer. Well, of course they are. But that's not the point. Can you think of a way of building this one block at a time? Yeah, in the back. Could you build something with a pile of dirt underneath it first? Very cool. If I had a prize, I would be happy to give it to you. Yeah. She said, "Build a pile of dirt first. "Build the arch over it, "then take the dirt away." So I did that, but not by a pile of dirt, but by building some other bricks. The ones that have red edges here. So you build them one at a time, then that's the framework, just like your idea of the pile of dirt, on which you can stack these outer bricks, and after you've got 'em all up there, you can start pulling those red-edged blocks out, and there's your keystone. So it is possible to do it one at a time. It didn't look like that initially because when I said, "One at a time," you all were thinkin' that it's each of those guys, and no others. But if you avail yourself of the simple device of adding and subtracting one at a time, you can do it. So I want to, that's a key idea in biology for understanding how delicate adaptations, complex adaptations, can evolve one step at a time by adding, but also by subtracting. So let me give you a biological example of the key, the arch story. So as you may remember from high school biology, chromosomes come in pairs in human beings and many, many other organisms. So that means if you have a pair of chromosomes here, and you look across the two chromosomes at the same location, you'll either find two copies of the gene, big A, or one copy of it, or zero of it. So we're thinking about a locus of, a location when this pair of chromosomes, it could be us, and which there are only two possible genes that could be there. Big A, and little A. So there are three possible states that any one of us could be in. We could be big A big A, we could be big A little A, or we could be little A little A. Those pairings of genes, there are three pairings that might exist, they're called genotypes. See there are two genes here, I hope this is ringing a bell. Two genes, big A and little A, diploid organism, chromosomes come in pairs, so therefore there are three possible genotypes that the organism might have. Let's think about what's gonna happen in a population as it evolves from 100 percent little A, and we drop a big A mutation into the population. And then in the goodness of time, big A completely replaces little A. Well, down here we drop, in the middle of the process, we'll find, of course, 50 percent little A and 50 percent big A. Here we have one percent big A, and so on. It's a very smooth process. Obvious. Next point. What happens at the level of pairs of genes, or the three genotypes, as you move from 100 percent little A to 100 percent big A? Well, in the beginning, if everybody is little, if little A is at 100 percent, then everybody has the little A little A genotype. And down at the end when every, when the gene big A is at 100 percent, that means that everybody in the population has two copies of big A. And in the middle, we expect the three genotypes to be formed, right? But let's go way back here. Let's start about, we've got, almost everybody has little A little A, and then we drop a big A mutation in there. Then that individ, then there'll be a heterozygote, and individual who's big A little A. So the way the population is going to evolve from 100 percent little A gene to 100 percent big A gene is by moving from everybody being little A little A, to most people being little A little A and a few people being big A little A, to a mixture of all three, and finally, to everybody being big A big A. But at the beginn, the point is, at the beginning of the evolution of big A starting here, big A is going to be found in individuals who have not another copy of big A, but rather a copy of little A. Because big A is so rare, it's going to be found next to a copy not of itself, but of little A. So let's think about that. Yes, so it's gonna happen as we move from here to here, and the Darwinian processes gradually go from 100 percent little A, to 99.5 percent little A, to 99 and so on and so. We don't make a jump, bang bang. We go gradually by the gradual change in gene frequency. The gradual change in genotype frequencies. Okay, so that's just what I've said. So now the question I want to ask is, suppose big A little A is not viable. Individuals who have one copy of itch, of each of those died at birth or before. Okay? So you start with everybody here. How can you get all the way over there, because as soon as you introduce a copy of big A in the population where everybody has only little A copies, that, big A is introduced next to a copy of little A, that's death. So that individual disappears, it can't reproduce. And so it can't send its genes into the next generation. So it looks like you can't get there from here if big A little A is non-viable. But you can. Here's how. Okay, I've been talking about the loc, a pair of chromosomes at which, which I'll call the A locus, the location, each individual has either two, one, or zero copies of big A. Now let's go to a different pair of chromosomes, and we'll look at a different loca, a location in that pair of chromosomes called the B locus. And it's kind of the same thing. You either have big B or little B at that locus. So there're three possible genotypes that you might have at that locus. Two copies of big B, one copy of big B, one of little, and two copies of little. And let's suppose that everybody in the population that we're talking about has little B little B, and this is the chance of an individual surviving if it has this pair of genotypes, this pair or genotypes, or this one. And as I said before, we're supposing in the example that if you had that genotype, you'd die at birth or before. So individuals in this box had zero chance of surviving to reproductive age, which means, what I said before, that if the population starts with everybody like that, there's no way that a gradual evolutionary process can take you from here to there. It can't take you from everybody having little A little A to everybody having big A big A, because there is death in between. Right? So you can't get there from here, it looks like. Just like in the Behe Paley idea, a complex adaptation won't evolve by nat, gradual natural selection because if it's delicate, adding something doesn't do the organism any good, and in this example, it actually harms it. You add a big A down here, and it makes your chance not 0.1 of surviving, but zero. But there is a way of doing it, by adding and subtracting. So now we're gonna consider not just what's going on at the A locus, we're gonna be considering what goes on at the B locus. There are three genotypes. The population starts here. Can it evolve away from a situation which everybody has two copies of little A and two copies of little B? Yes. It can go from here to there because big B is advantageous in this context, and then it can go all the way up there, with big B going all the way to 100 percent. And then it can go over there, over there, and then you're all the way down there. Doesn't this look like an arch? (audience murmurs and laughs) Okay. So I hope you see the analogy between this, this is a little harder. This is a genetics example. I hope you see the analogy between this and that. You can get a complex structure to evolve by adding and subtracting. And that's what you're doing in this genetic example. You're adding, you're starting here. You're adding B into the population, and then you're subtracting it out again. And that's how natural selection, a gradual process can take you from here to there, not by crossing this value, that's a no-go zone. But by going that way, circuitously. By adding and subtracting. So that's a key idea, it's not the only idea, but it's a key idea in understanding why Behe was wrong. Why Paley was wrong. Paley couldn't have known about genetics, or about this idea about natural selection. But it's out there in biology. So when biologists talk about what's wrong with intelligent design theory, this is one of the ideas they bring up. There're other things. But that's the one I wanted to talk about today. So let me summarize what I just told you about the organismic design argument. The design of this ar, this version of the design argument says that complex adaptations can't be created by a mindless process. And then I told you a bit about Darwin's theory that natural selection is a gradual process, and I tried to get you to see that what the problem was, that Darwin was talking about, he said that if there was any structure that couldn't be created by the, the small and numerous additions of changes, small changes, each favorable to the organism, my theory would go up in smokes, he said. And I don't think, and then he said, "I don't think there are structures like that." But you see, he's posing the problem in just the way that Behe or Paley would want to think about it. The solution to the problem, according to biologists now, and Darwin back then, is not, "Oh, it was an intelligent designer," but rather to think about this adding and subtracting idea as a device for getting complicated structures to evolve when it doesn't look like they could when you only look at the parts that are present now. Okay, that's one argument down and the next one to go. So now we're gonna talk about physics, not about biology. The fine-tuning argument concerns the physical constants. As I mentioned, they have this amazing feature that if any of these constants were even slightly different in value, like by half a percent, or you know, a hair, life would, the universe would be incompatible with the existence of life. The whole universe! Not just Earth, now. So why are the physical constants showing this beautiful property that allows the universe to be right for life? And you know what the design argument says about that. It had to be an intelligent designer who created the universe in this way. So but how do we explain this? And what I want to do is, before I get to different answers and ways of thinking about that question additional to the intelligent design answer, I want to offer a tool that'll help us to understand the reasoning that goes on when people talk about fine-tuning. Both people in favor of this argument that I just described, and people who are critical of it. Okay, so... I'll describe the tool by giving you an example. Now this could never be an example about UW Madison. In some other university. Not necessariy in the midwest. A philosophy professor assigns an essay problem to her students, and two of the students hand in identical essays. Now, this professor that I'm talking about is, does not jump to hasty conclusions. No fire extinguisher is needed for this professor that I'm talking about. So rather than jumping to conclusions prematurely, the professor thinks about two possible explanations. Two possible hypotheses. The first one is the hypothesis that the students cheated. They plagiarized from a file that they found together on the internet. And the second hypothesis, let's be open-minded, is that there was no collusion, there was no cheating, but rather the students worked separately and independently, and just happened, by an amazing coincidence, to come up with papers that were identical. Now, I hope you are as cynical as I am, and think that the evidence strongly favors the first hypothesis over the second. It doesn't prove that it's gotta be true, but it's pretty serious evidence in favor of H1 against H2. Well here's a principle that expresses that idea. It's called, in statistics, the Law of Likelihood. You have an observation, O, and you have two possible hypotheses, two possible explanations that you want to consider, of that observation, and the Law of Likelihood tells you that the observation favors H1 over H2 when this is true, what does that mean? This says that the probability of the observations given H1 is greater than the probability of the observations given H2. And that's what's going on in this example. Look, if H1 were true, it wouldn't be that surprising the papers matched. Whereas if H2 were true, it would be extremely improbable. Almost a miracle, maybe we'd want to say, that the papers matched. And so the professor, and you, and I are right to conclude that the observations I'm talking about favor one of the hypotheses over another. Here's another example. You've got an urn, it's filled with balls. Each ball has a color. You have two hypotheses you want to consider about the composition of the urn. The first says that the urn has 50 percent green balls, the second says it has two percent. You then draw 100 balls from the urn, 60 of them are green. What does this observation tell you about the two hypotheses? It does not prove that H1 is true. It does not prove that H2 is false. But the observation seems to favor, strongly favor, H1 over H2, because the observations are rather probable if H1 is true, the observations are extremely improbable if H2 is true. Law of Likelihood again. Okay, so that's the tool we want to use in thinking about fine-tuning. Okay. Now, let's suppose that if an intelligent designer made the universe, it is highly probable that the constants, the physical constants I mentioned, would be right for life. They would have the values in that narrow range that permits life to exist in the, in the universe. We're assuming here that the designer in question likes the idea of life. I mean, if you're thinkin' about an intelligent designer who hates life, then that probability would be zero, right? But let's not go there. Let's think about an intelligent designer who wants life to exist. He's got, he or she or it, has got the power to bring that about. So the probability of the constants being right, if the intelligent design hypothesis is true, is very high. Well, what can we conclude from that? Does that show that the observation that the constants are right for life is strong evidence for intelligent design? What does the Law of Likelihood tell us we should think about this question? Well, it's a simple fact about the Law of Likelihood that it does not talk about evidence as it bears on a single hypothesis in isolation. It's a comparative principle. You've gotta have at least two hypotheses, and the question is whether the observation favors one over the other. So it ain't good enough to just say, "This has a high probability." You've gotta consider what the probability would be of the constants being right for life if some alternative hypothesis were true. And then we could compare the two likelihoods, just like we did in the student plagiarism case, just like we did in the urn and the green balls case. So let's talk about some alternatives to intelligent design, and do a Law of Likelihood analysis. Okay, so here's a hypothesis we'll consider. It's the chance hypothesis. It says that there's a single universe, the one we live in, and the values of the physical constants are all determined by chance. Namely, it could have this value with the same probability it has this value, all possible values of the physical constants have the same probability, and the chance hypothesis says that's why the constants are right for life. And what we'd like to do is compare the probability of the constants being right for life if the intelligent design hypothesis is true, with the probability the constants are right for life if the chance hypothesis is true. Notice that in both cases, we're talking about the probability that the observations are as they are, under two different hypotheses. And I hope you agree with me that the first is a bigger value than the second. We already started off by saying this has got a high value. To say that this is, this is a tiny value, it's not zero. But if you're just gonna determine the values by a kind of random process where every outcome has the same probability as every other, and if there're a billion possible settings of the physical constants, where one of them in gonna be right for life, the probability of getting that outcome is one in a billion! Which is a pretty small number. It's not zero, but it's pretty small. So the Law of Likelihood says, and this is what defenders of the fine-tuning argument say, this observation that physics gives us about the universe we live in strongly favors intelligent design over the chance hypothesis. It doesn't prove that this must be true and that must be false, but it's strong evidence favoring one over the other. So that's one alternative hypothesis. Alternative to intelligent design. Here's another hypothesis of physics. It's called the multiverse hypothesis. There are many universes. We live in one. And each universe has its physical constants set by this chance process that I mentioned before, but there are zillions of universes in the multiverse hypothesis and so, one of them is probably going to be right for life. Maybe two. But not that many. Depends how many, how multi the multiverse is. So let's compare these two. And I just said, "Well, if the multiverse hypothesis is true, "it's rather probable that some universe or other "would be right for life." But that doesn't show that this is bigger than that. Because the observation we're talking about here is not that some universe or other in the multiverse is right for life. We're talking about our universe. So don't ask yourself the question, "If the multiverse "hypothesis is true, how probable is it "that some universe or other will be right for life?" That's the wrong question. Ask yourself the question, "What's the probability "that this universe would be right for life "if the multiverse hypothesis were true?" And once again, the answer is not very! It's like one in a zillion. So again, the intelligent design hypothesis is favored over the mult, over an alternative in this case, the multiverse hypothesis. So, so far I've talked about two alternatives to the intelligent design hypothesis, and in both cases, intelligent design beats the pants off of the alternative, where the alternative is a mindless process that involves chance. And now I want to introduce a new wrinkle, a new idea. It's called an observation selection effect. Which is why we're gonna (grunts) try to describe this clearly, and then we'll take it back to the fine-tuning argument to see what its implications are. So here's an example, not from physics or biology, of an observation selection effect. So you're using a net to fish in a lake. You leave the net in overnight. You come back, and you look in the net, and you notice that all the fish in the net are more than 10 inches long. And that observation, you think, might help you to compare, to evaluate how plausible these two hypotheses are. The first hypothesis is all the fish in the lake are over 10 inches long. And the second says only 10 percent of them are. And it seems intuitive that... If that were true, then your observations would be very probable, whereas if that hypothesis were true, this would be very improbable. So it seems like, you know, what's the problem here? The observations of all these 10-inch or longer fishes in your net favors H1 over H2 in the sense of the Law of Likelihood. But then! You notice something! You look at this net you've got, and the holes are all 10 inches across. And you say, "Oooooh!" This means that you were bound to observe fish that are all at least 10 inches long, regardless of what the lake's composition is like. Regardless of whether all of the fish are at least 10 inches long, or only 10 percent of them are. So what you want to say about this example is that given that you used this net with the peculiar structure I just mentioned, the probability is the same that you'd get this outcome regardless of whether H1 or H2 is true. So you started off thinking that this inequality was true, you then look at the net, which has 10-inch wide holes, and you end up thinking the inequality was wrong. It's an equality, the Law of Likelihood is then telling you that this observation does not favor H1 over H2. The net has induced an observation selection effect. The technique you used to look at the lake, namely, this net you used, has biased your observations, making it inevitable that you'd observe what you observed regardless of which hypothesis is true. So that's called an observation selection effect. I hope you can guess what this has to do with fine-tuning. We exist when we observe the physical constants, we are living things. It's inevitable that we'll see that the constants have a value compatible with the existence of life, because we're alive. And so, given that we exist, the observation that the constants are right for life do not favor intelligent design over chance. It's not a high probability versus one in a billion. It's two numbers, whatever they are, that are about the same. Maybe they're both one. So given that we exist, we're gonna get this outcome regardless of whether the universe was produced by intelligent design or by chance. And the same is true is, if we consider the multiverse hypothesis instead. So our existence as living things is like the net with 10-inch holes in it in the fishing example. Our existence induces an observation selection effect, turning what you might have thought would be an inequality into an equality. Just like we noticed here. Okay, so let me summarize. So the observation is kind of, it's amazing. It's a striking fact. You look at all these physical constants, they have this value, this value, this value, and you then notice if they were even a tiny bit different, life couldn't exist in the whole universe. And I told you about the Law of Likelihood, and how it allows you to evaluate competing hypotheses, and I talked about these two competitors, the chance hypothesis and the multiverse hypothesis. And on the face of it, it looked like, if you use the Law of Likelihood on this problem, what you're gonna end up saying is the fact that the constants are right for life strongly favors intelligent design over each of these. But then I talked about the idea of an observation selection effect, and argued that once we think about that, we see that there is no such inequality. The observational outcome, that the constants are right for life, that would happen, given that we exist, regardless of whether this universe were the reas, were made by an intelligent designer or by chance. So here's my last comment about both the organismic and the cosmological design argument. Creationism on the one hand, and the fine-tuning argument on the other. I think both of these arguments fail to establish the existence of God. But that doesn't mean that you shouldn't believe in God. And for at least two reasons. First of all, these are just two arguments. There might be other arguments that establish the existence of God in a fully satisfactory way, and so what if these don't work? Maybe there're others that do. But more fundamentally, I have to come back to something I mentioned briefly at the beginning. Rather than thinking about scientific arguments for the existence of God, maybe you wanna say, "Look. "Believing in God is not a matter of evidence, "but a matter of faith," and if that's how you think about it, it doesn't matter whether the fine-tuning argument fails. It doesn't matter whether creationism is wrong as a scientific hypothesis. What matters is faith, not evidence and arguments of the kind I've explored. So thanks. (applause)
Search University Place Episodes
Related Stories from PBS Wisconsin's Blog

Donate to sign up. Activate and sign in to Passport. It's that easy to help PBS Wisconsin serve your community through media that educates, inspires, and entertains.
Make your membership gift today
Only for new users: Activate Passport using your code or email address
Already a member?
Look up my account
Need some help? Go to FAQ or visit PBS Passport Help
Need help accessing PBS Wisconsin anywhere?
Online Access | Platform & Device Access | Cable or Satellite Access | Over-The-Air Access
Visit Access Guide
Need help accessing PBS Wisconsin anywhere?

Visit Our
Live TV Access Guide
Online AccessPlatform & Device Access
Cable or Satellite Access
Over-The-Air Access
Visit Access Guide
 Passport
Passport









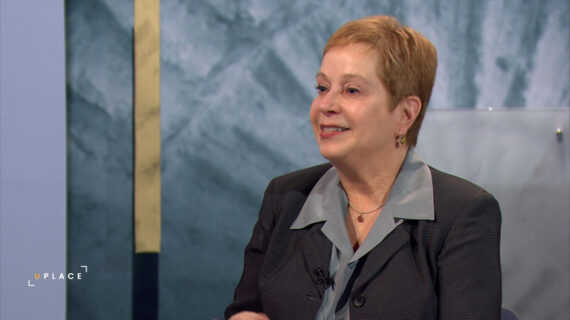







Follow Us